🔒 문제
https://school.programmers.co.kr/learn/courses/30/lessons/12940
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
문제 설명
두 수를 입력받아 두 수의 최대공약수와 최소공배수를 반환하는 함수, solution을 완성해 보세요. 배열의 맨 앞에 최대공약수, 그다음 최소공배수를 넣어 반환하면 됩니다. 예를 들어 두 수 3, 12의 최대공약수는 3, 최소공배수는 12이므로 solution(3, 12)는 [3, 12]를 반환해야 합니다.
제한 사항- 두 수는 1이상 1000000이하의 자연수입니다.
| n | m | return |
| 3 | 12 | [3, 12] |
| 2 | 5 | [1, 10] |
입출력 예 #1
위의 설명과 같습니다.
입출력 예 #2
자연수 2와 5의 최대공약수는 1, 최소공배수는 10이므로 [1, 10]을 리턴해야 합니다.
🔓 풀이
🔑 문제 해결 / 코드
def gcd(a, b):
if a % b == 0:
return b
return gcd(b, a % b)
def solution(n, m):
gcd_n = gcd(n, m)
return [gcd_n, int(n * m / gcd_n)]🍀 story
최대공약수(gcd)와 최소공배수(lcm)을 구하는 방법은 각각의 성격만 안다면 비교적 쉽게 알고리즘을 작성할 수 있다.
최근에 재귀함수를 배우면서 유클리드 호제법을 접할 기회가 있어서 그 방법을 사용했다.
A와 B의 최대공약수, 최소공배수 구하기
최대공약수(GCD)
a와 b의 최대 공약수는 a를 b로 나눈 나머지(r)와 b의 최대공약수와 같다. (a > b)
gcd(a, b) = gcd(b, r)
이 과정을 반복하다보면 나머지가 0이 될때가 있는데 이때 나누는 수가 a와 b의 최대공약수다.
공식에서는 a > b인 경우를 가정하지만 a < b일때 a를 b로 나눈 나머지는 a이므로 자연스럽게 a, b의 위치가 바뀌게 된다.
최소공배수(LCM)
최소공배수는 AB = GL의 공식이 성립하는데 글로 설명하자니 가독성이 안좋아서 패드를 꺼내 끄적끄적 해봤다.
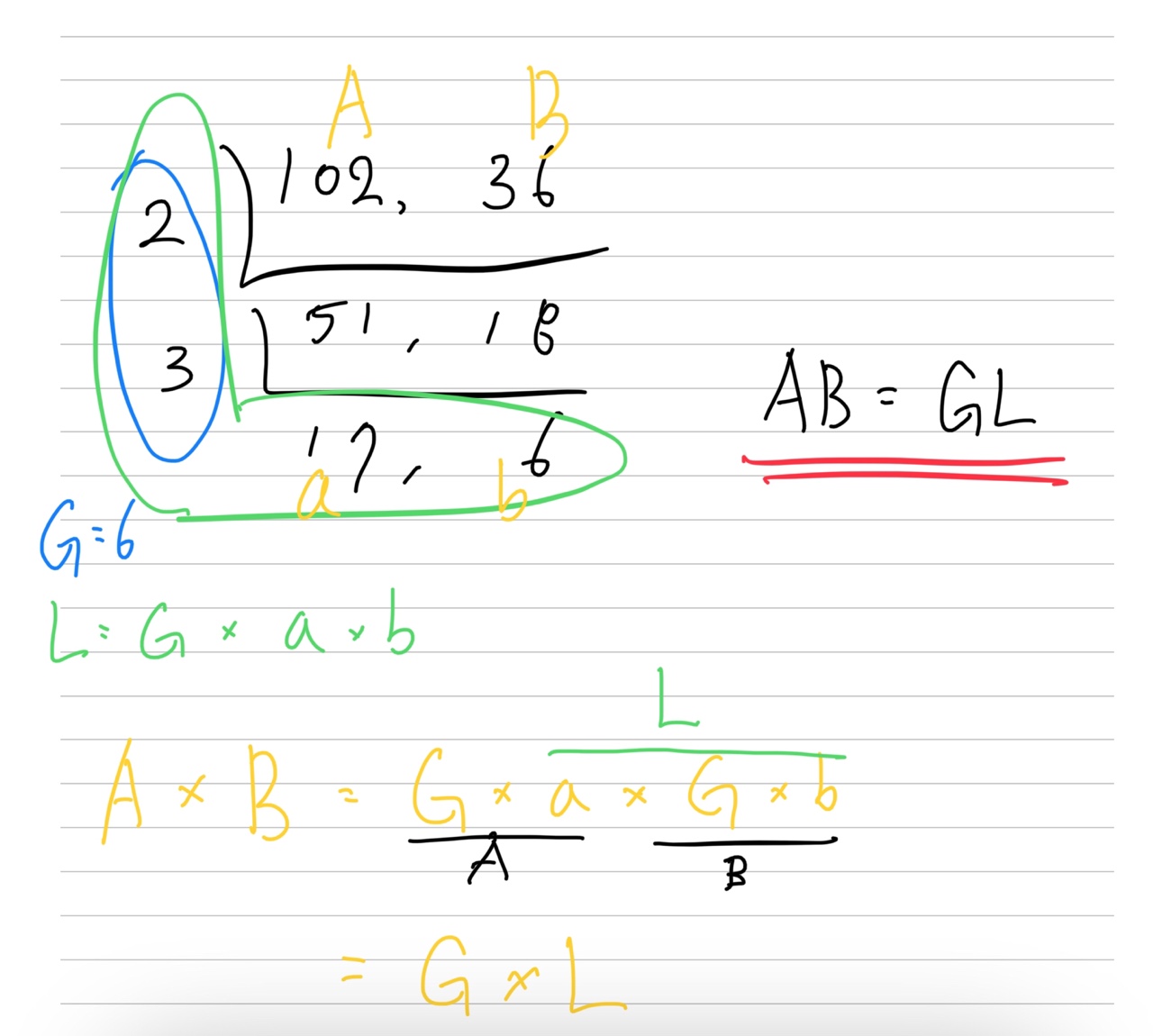
위 예시를 보자
최대공약수와 서로소인 a를 곱하면 A(102)가되고 b를 곱하면 B(36)이 되는데 A와 B를 곱하면 G * a * G * b 가 성립하고 G * a * b 는 최소공배수(L)와 동일하므로 AB = GL이 성립한다.
따라서 최대공약수만 구해진다면(유클리드 호제법) A와 B를 곱하고 G로 나눠주면 최소 공배수가 된다.
L = AB/G
'알고리즘' 카테고리의 다른 글
| [프로그래머스] 기능개발_Python level2(스택/큐) (0) | 2022.08.11 |
|---|---|
| [프로그래머스] 123 나라의 숫자_Python level2 (0) | 2022.08.10 |
| [프로그래머스] 오픈채팅방_Python level2 (0) | 2022.08.02 |
| [프로그래머스] 소수 찾기_Python (0) | 2022.07.27 |
| [프로그래머스] 자연수 뒤집어 배열로 만들기_Python (0) | 2022.07.18 |